.png "Menu")
Anisotropic Diffusion in Image Processing
Images provide insight into the world, our lives, places, things e.t.c Human beings have the implicit ability to understand and make sense of an image both semantically and syntactically. Thus we are able (assuming I am human), to make visual conclusions easily, from visual information presented in images. This is not the same for Artificial Intelligence as the ease eludes it.
Image processing is a science that facilitates the world with algorithms that can extract information embedded in images with the eventual aim to make sense of such information. However, factors such as inefficient image capture e.t.c introduces noise into images. It is therefore important to be able differentiate noise from information. Filtering techniques help in this separation.
Gaussian filtering is a process of noise elimination in images by the convolution of an image with a Gaussian. This Gaussian of scale or standard deviation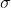 
, isotropically blurs the image thereby reducing the noise. Since noise exists in images in high frequencies, this replaces every pixel by the weighted combination of its neighbours. The weights are determined by 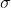which also determines the window size for the convolution. Mathematically, a Gaussian in 2D corresponds to,
=&space;&space;%5Cfrac%7B1%7D%7B2%5Cpi%5Csigma%5E2%7De%5E%7B-%5Cfrac%7Bx%5E%7B2%7D+y%5E%7B2%7D%7D%7B2%5Csigma%5E%7B2%7D%7D%7D "G(x) = \frac{1}{2\pi\sigma^2}e^{-\frac{x^{2}+y^{2}}{2\sigma^{2}}}")
This formula states that a concentration gradient creates a flux which aims to compensate for the concentration gradient. During this flow, no new mass is created or destroyed. The mathematics savvy reader would be drawn to the fact that this can be represented using the continuity equation
 "\partial u_{t} = -div (D\nabla u)")
The diffusion tensor 
is a positive definite symmetric matrix. When it is scalar, it corresponds to isotropic diffusion all through the image such as using a Gaussian. The real task is finding that would allow for the blurring of homogeneous regions while protecting the edges. Perona and Malik solved that by introducing a dependence of 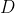on the gradient of the image. The gradient of the image, is a rough estimate of edges. So, if we have a diffusion tensor that is dependent on the gradient, we hence can create a non uniform diffusion process that avoids the edges (Pretty obvious isn't it?)
 "\partial u_{t} = -div (g|\nabla u|^{2}\nabla u)")
%5E%7B2%7D%7D "g|\nabla&space;u|^{2} = \frac{1}{1 + (\frac{|\nabla&space;u|}{K})^{2}}")
and
%5E%7B2%7D%7D "g|\nabla&space;u|^{2} = e^{-(\frac{|\nabla&space;u|}{K})^{2}}")
It is however generally known that this corresponds to low pass filter, which would blur the image. Thus, reducing the noise and also, edges in the data which correspond to high frequency information. Edges are very important in image processing just as they are important in human vision because they correspond to object boundaries. These boundaries hence define the localised object within the image scene. The blurring of edges is thus an undesirable effect. Another undesirable quality is, due to the fact that a Gaussian filter replaces a pixel value by the weighted combination of its neighbour pixels, there is an edge shift. So the eventual location of the edge is not the correct location of it. Assume we are designing the vision system of a Robot and we decide to filter the images that come through using a Gaussian, this shift in edge (if large), would make the Robot to bump into walls and objects.
To combat these effects, Perona and Malik introduced a new filter that blurs homogeneous spaces whilst not blurring the edges.
Anisotropic diffusion filter, introduced by Perona and Malik, is built on the Mathematical formulation of the Gaussian filter which can be correlated to the Diffusion law.
Ficks law of equilibration as defined by the formula.
To combat these effects, Perona and Malik introduced a new filter that blurs homogeneous spaces whilst not blurring the edges.
Anisotropic diffusion filter, introduced by Perona and Malik, is built on the Mathematical formulation of the Gaussian filter which can be correlated to the Diffusion law.
Ficks law of equilibration as defined by the formula.
This formula states that a concentration gradient creates a flux which aims to compensate for the concentration gradient. During this flow, no new mass is created or destroyed. The mathematics savvy reader would be drawn to the fact that this can be represented using the continuity equation
If we plug Ficks law into the continuity equation, we get the diffusion law which would be
As is observed, the new diffusion tensor is dependent on the gradient and thus, provided the function is chosen carefully, can avoid the blurring of the edges. Two functions were thus proposed
Those who are familiar with the paradigms of machine learning would immediately recognise the fact that these functions gives weights to the diffusion tensor, scaling this weight based on the edge strength.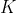 
is called the conduction parameter. From the analysis of the above equation, it can be inferred that 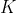helps the generation of weights by regularising the gradient matrix. This helps to place emphasis on how strong the edge should be before it avoided in the filtering or diffusion process. This parameter is important as noise is scaled in the gradient of an image, so 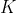should be optimised to separate true edges from false; men from boys. Now that we have defined the mathematics for anisotropic diffusion, we go on to implement it in python. Not in this post though, in the next one.
0 comments :